Lesson 4: Check Your Knowledge

To solve the following problems, use AH 505 to look up factors in the compound interest tables. The solution is given immediately following each problem. The option to print the problems with or without the answers is provided using the buttons below.

Print ProblemsPrint Problems with Answers

Open All Solutions Close All Solutions

Problem 1

Calculate the future value of each payment (PMT) listed below using the future worth of $1 per period (FW$1/P) factors in AH 505:

Row	PMT (Periodic Payment)	# periods (years)	Annual Rate (%)
1	$1,000	5	4
2	$100	40	1
3	$2,000	20	2
4	$1,000	10	5
5	$1,000	12	1

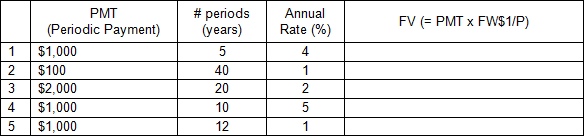
Solution

To solve, calculate the future value of each payment amount by multiplying the amount by the future worth of $1 per period factor found in the AH 505 annual compound interest tables for the given interest rate and term.

FV = PMT × FW$1/P
FV = $1,000 × 5.416323 (AH 505, page 25, column 2)
FV = $5,416.32
FV = PMT × FW$1/P
FV = $100 × 48.886373 (AH 505, page 13, column 2)
FV = $4,888.64
FV = PMT × FW$1/P
FV = $2,000 × 24.297370 (AH 505, page 17, column 2)
FV = $48,594.74
FV = PMT × FW$1/P
FV = $1,000 × 12.577893 (AH 505, page 29, column 2)
FV = $12,577.89
FV = PMT × FW$1/P
FV = $1,000 × 12.682503 (AH 505, page 13, column 2)
FV = $12,682.50

Problem 2

You invest $2,000 in an IRA account at the end of each year for 20 years. Assuming an annual interest rate of 8%, with annual compounding, how much will you have at the end of 20 years?

Solution

To solve, calculate the future worth of a series of equal future payments using the FW$1/P factors in annual compound interest tables in AH 505. Multiply the payment amount by the FW$1/P factor for the interest rate of 8% and 20 year term.

FV = PMT × FW$1/P (8%, 20 yrs, annual)
FV = $2,000 × 45.761964 (AH 505, page 41, column 2)
FV = $91,523.93

Problem 3

A property generates $15,000 annually over a seven-year period. At the end of each year, the income is deposited into an account that pays interest of 6 percent, compounded annually. How much will be in the account after seven years?

Solution

To solve, calculate the future worth of a series of equal future payments using the FW$1/P factor in the annual compound interest tables in AH 505. Multiply the payment amount by the FW$1/P factor for the interest rate of 6% and 7 year term.

FV = PMT × FW$1/P (6%, 7 yrs, annual)
FV = $15,000 × 8.393838 (AH 505, page 33, column 2)
FV = $125,908

Problem 4

A friend plans to invest $2,000 in an IRA account at the end of each year, starting when she is 25 years old and continuing until her expected retirement at age 65 (40 years later). She expects to earn an annual return of 8% a year on her investment. What is the expected value of the account on her retirement date?

Solution

To solve, calculate the future worth of the annual deposits using the FW$1/P factor in the annual compound interest tables in AH 505. Multiply the payment amount by the FW$1/P factor for the interest rate of 8% and 40 year term (65 less your current age of 25).

FV = PMT × FW$1/P (8%, 40 yrs, annual)
FV = $2,000 × 259.056519 (AH 505, page 41, column 2)
FV = $518,113.04

Problem 5

You deposit $1,000 at the end of each month, earning an annual rate of 12% with monthly compounding. How much will you have at the end of 15 years?

Solution

To solve, calculate the future worth of the monthly deposits using the monthly FW$1/P factor in the monthly compound interest tables in AH 505. Multiply the payment amount by the FW$1/P factor for the interest rate of 12% and 15 year term.

FV = PMT × FW$1/P (12%, 15 yrs, monthly)
FV = $1,000 × 499.580198 (AH 505, page 56, column 2)
FV = $499,580.20

Problem 6

Johnny will begin college in 18 years. If you deposit $100 at the end of each month for the next 18 years in Johnny's college fund, how much will Johnny have for college? Assume an earnings rate of 9% compounded monthly.

Solution

FV = PMT × FW$1/P (9%, 18 yrs, monthly)
FV = $100 × 536.351674 (AH 505, page 44, column 2)
FV = $53,635.17

Next Lesson