Lesson 5: Check Your Knowledge

To solve the following problems, use AH 505 to look up factors in the compound interest tables. The solution is given immediately following each problem. The option to print the problems with or without the answers is provided using the buttons below.

Print ProblemsPrint Problems with Answers

Open All Solutions Close All Solutions

Problem 1

Using the sinking fund factor (SFF), given the future value provided below, solve for the amount of the periodic (annual) payment that will compound to that future value.

Row	FV	n (years)	Annual Rate (%)
1	$10,000	5	4
2	$150,000	40	1
3	$25,000	20	2
4	$50,000	10	5
5	$15,000	12	1

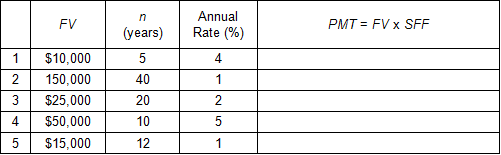
Solution

To solve, calculate the amount of payment if made annually needed to arrive at each future value given by multiplying the amount given by the Sinking Fund Factor found in the AH 505 annual compound interest tables for the given interest rate and term.

PMT = FV × SFF
PMT = $10,000 × 0.184627 (AH 505, page 25, column 3)
PMT = $1,846.27
PMT = FV × SFF
PMT = $150,000 × 0.020456 (AH 505, page 13, column 3)
PMT = $3,068.40
PMT = FV × SFF
PMT = $25,000 × 0.041157 (AH 505, page 17, column 3)
PMT = $1,028.93
PMT = FV × SFF
PMT = $50,000 × 0.079505 (AH 505, page 29, column 3)
PMT = $3,975.25
PMT = FV × SFF
PMT = $15,000 × 0.078849 (AH 505, page 13, column 3)
PMT = $1,182.74

Problem 2

Windpower Inc. has just issued bonds with a face value of $100 million that become due in 25 years. The bond contract contains a provision that Windpower must make equal payments at the end of each year into a sinking fund that will be used to retire the bonds after 25 years. How much must Windpower set aside each year if the annual interest rate is 7%?

Solution

To solve, calculate the annual payment amount using the annual sinking fund factor. Multiply the face value of the bonds using the SFF using the factors in AH 505 annual compound interest tables with an annual rate of 7% and 25 year term.

PMT = FV × SFF (7%, 25 yrs, annual)
PMT = $100,000,000 × 0.015811 (AH 505, page 37, column 3)
PMT = $1,581,100.00

The annual payment (end of each year) would be $1,581,100.00.

Problem 3

Johnny will enter college in 10 years. At that time, you would like to have a balance of $100,000 in his college fund. Assuming an earnings rate of 8%, how much must you invest at the end of each month to fund Johnny's education?

Solution

To solve for the monthly payment amount, multiply the desired amount after 10 years by the SFF for monthly interest rate of 8% and a 10 year term.

PMT = FV × SFF (8%, 10 yrs, monthly)
PMT = $100,000 × 0.005466 (AH 505, page 40, column 3)
PMT = $546.60

The monthly investment (end of each month) would be $546.60.

Problem 4

You expect to replace the roof of your investment property in 15 years. The estimated cost of the replacement is $800,000. Assuming that you can earn an annual rate of 4%, how much should you set aside at the end of each year in order to fund the future roof replacement?

Solution

To solve for the annual payment amount, multiply the future value (replacement cost) using the SFF in AH 505 annual compound interest tables with an interest rate of 4% and 15 year term.

PMT = FV × SFF (4%, 15 yrs, annual)
PMT = $800,000 × 0.049941 (AH 505, page 25, column 3)
PMT = $39,953

The annual investment (end of each year) would be $39,952.80.

Problem 5

Pete likes to plan ahead. When he retires 30 years from now, he would like to have $1,000,000 in his 401k retirement account. If he expects to earn an annual rate of 15%, how much should he deposit at the end of each month in order to reach his goal?

Solution

To solve, calculate the monthly payment amount by multiplying the future value (desired amount in 30 years) by the SFF in the AH 505 monthly compound interest tables based on the expected 15% annual interest rate and 30 year term.

PMT = FV × SFF (15%, 30 yrs, monthly)
PMT = $1,000,000 × 0.000144 (AH 505, page 68, column 3)
PMT = $144.00

The monthly deposit (end of each month) would be $144.00.

Next Lesson