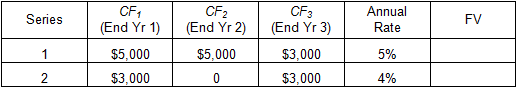Lesson 2: Future Worth of $1
Check Your Knowledge
In order to solve the following problems you will need to refer to AH 505 to look up the factors in the compound interest tables. Before you start, please print the problems using the "Print Questions" button below so you can work through the problems on your own. After you work through the problem, the solution can be viewed by clicking on the blue plus sign immediately following the question. Additionally, when you have completed all the problems, you may print all of the solutions using the "Print Questions with Answers" button below.
Problem 1
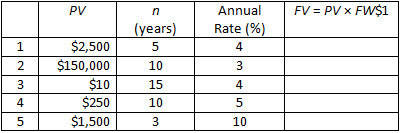
Calculate the future value (FV) of each present value (PV) listed below using the future worth of $1 (FW$1) factors in AH 505:
Solution 

Solution:
To solve, calculate the future value of each present value amount by multiplying
the amount by the future worth of $1 factor found in the AH 505 annual compound interest tables for the given interest rate and term
FV = PV × FW$1
FV = $2,500 × 1.216653 (AH 505, page 25, column 1)
FV = $3,041.63
FV = PV × FW$1
FV = $150,000 × 1.343916 (AH 505, page 21, column 1)
FV = $201,587.40
FV = PV × FW$1
FV = $10 × 1.800944 (AH 505, page 25, column 1)
FV = $18.01
FV = PV × FW$1
FV = $250 × 1.628895 (AH 505, page 29, column 1)
FV = $407.22
FV = PV × FW$1
FV = $1,500 × 1.331000 (AH 505, page 49, column 1)
FV = $1,996.50
Problem 2
You have a choice of investing in either of two accounts:
- Account A earns an annual rate of 5% with annual compounding
- Account B earns an annual rate of 5.25% at simple interest
You plan to invest $10,000 in one of the accounts today and withdraw the funds 4 years later. In which account should you place your funds?
Solution 

Solution:
The best choice is the account that will have the most money at the end of the 4 year period.
To solve, calculate the future value of each alternative and select the account with the higher future value.
Account A
FV = PV × FW$1 (5%, 4 yrs, annual)
FV = $10,000 × 1.215506 (AH 505, page 29, column 1)
FV = $12,155.06
Account B
FV = PV + FW$1 (5.25%, 4 yrs) (simple interest)
FV = $10,000 + ($10,000 × 5.25% × 4 yrs)
FV = $10,000 + $2,100
FV = $12,100.00
Because account A produces the higher future value, it is preferred.
The annual compounding in account A more than compensates for the higher rate at simple interest in account B.
Problem 3
If you deposit $10,000 in an account that pays an annual interest rate of 7%, how much money will you have at the end of:
- 10 years?
- 20 years?
- 40 years?
Solution 

Solution:
To solve, calculate the future value of the deposited amount at the end of each term using the future worth of $1 factors in the
AH 505 annual compound interest tables with an annual rate of 7%.
After 10 years:
FV = PV × FW$1 (7%, 10 yrs, annual)
FV = $10,000 × 1.967151 (AH 505, page 37, column 1)
FV = $19,671.51
After 20 years:
FV = PV × FW$1 (7%, 20 yrs, annual)
FV = $10,000 × 3.869684 (AH 505, page 37, column 1)
FV = $38,696.84
After 40 years:
FV = PV × FW$1 (7%, 40 yrs, annual)
FV = $10,000 × 14.974458 (AH 505, page 37, column 1)
FV = $149,744.58
Problem 4
You deposit $10,000 today in an account that earns an annual rate of 7.5%. At the end of 5 years,
how much interest on interest will the account have earned?
Hint: The amount of interest on interest is the difference between the future value at
compound interest and the future value at simple interest.
Solution 

Solution:
Determine the future value at compound interest:
FV = PV × FW$1 (7.5%, 5 yrs, annual)
FV = $10,000 × 1.435629 (AH 505, page 39, column 1)
FV = $14,356.29
Determine the future value at simple interest:
FV = PV + (PV × 7.5% × 5 yrs)
FV = $10,000 + ($10,000 × 7.5% × 5 yrs)
FV = $10,000 + $3,750
FV = $13,750.00
Amount of interest on interest = $14,356.29 - $13,750.00 = $606.29
Problem 5
You have just purchased an investment property for $400,000. You expect the value of the property to increase at an annual
compound interest rate of 8% over the next 10 years. How much do you expect the property to be worth after 10 years?
Solution 

Solution:
To solve, calculate the expected future value of the investment property using the future worth of $1 factor in the AH 505 annual
compound interest tables for 10 years at an annual rate of 8%.
FV = PV × FW$1 (8%, 10 yrs, annual)
FV = $400,000 × 2.158925 (AH 505, page 41, column 1)
FV = $863,570.00
You expect the property to be worth $863,570.
Problem 6
Assuming all cash flows (CF) occur at the end of each year, determine the future values of each of the following two series of cash flows:
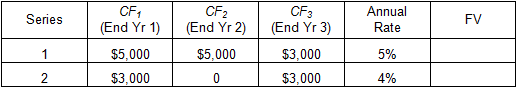
Solution 

Solution:
To solve, calculate the future value of the cash flow at the end of each year using the future worth of $1 factors in the AH 505 annual compound
interest tables with an annual rate of 5% for series 1 cash flows and 4% for series 2, and then add the future values of each cash flow in the series.
The sum is the future value of the series of cash flows.
FV of Series 1 (AH 505, page 29, column 1)

FV of Series 2 (AH 505, page 25, column 1)