Time Value of Money – Six Functions of a Dollar
Lesson 7 – Periodic Repayment

The PR is the payment amount, at periodic interest rate i and number of periods n, in which the present worth of the payments is equal to $1, assuming payments occur at the end of each period.

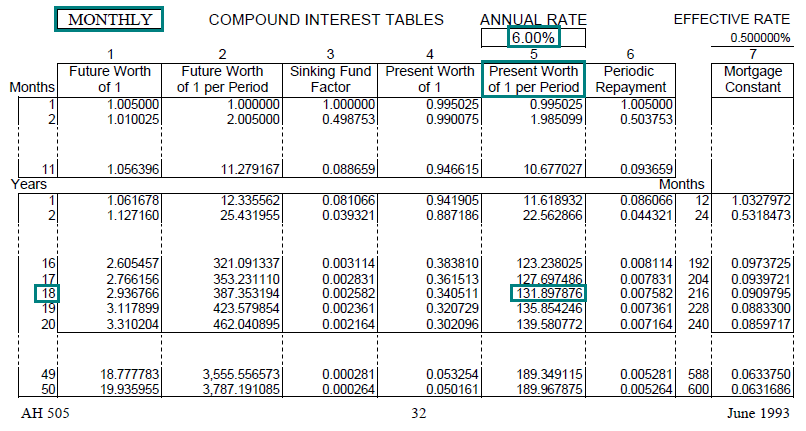
The PR is also called the loan amortization factor or loan payment factor, because the factor provides the payment amount per dollar of loan amount for a fully amortized loan. The PR factors are in column 6 of AH 505 (opens in a new tab).

The PR can be thought of as the “opposite” of the PW$1/P which was discussed in Lesson 6; mathematically, the PR and the PW$1/P factors are reciprocals as shown below:

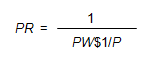
Conceptually, the PW$1/P factor provides the present value of a future series of periodic payments of $1, whereas the PR factor provides the equal periodic payments the present value of which is $1.

If a loan is repaid over its term in equal periodic installments, the loan is fully amortized. In a fully-amortized loan, each payment is part interest and part repayment of principal. Over the term of a fully amortized loan, the principal amount is entirely repaid.

From the standpoint of the lender, a loan is an investment. In an amortized loan, the portion of the payment that is interest provides the lender a return on the investment, and the portion of the payment that is principal repayment provides the lender a return of the investment.

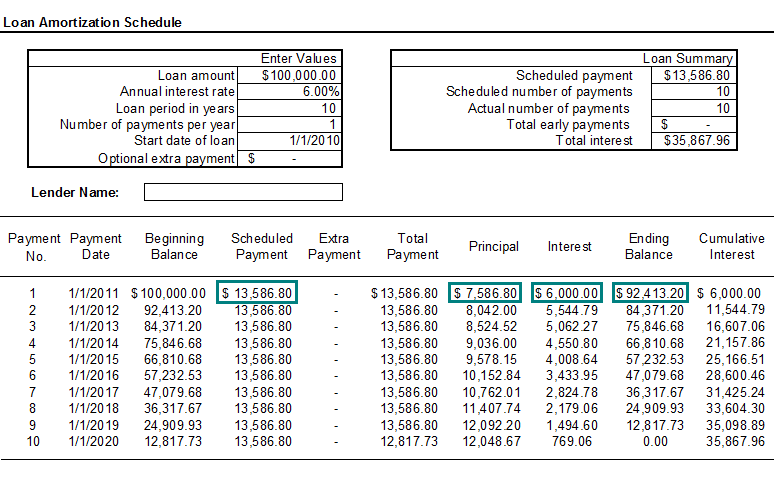
An amortization schedule shows the distribution of loan payments between principal and interest throughout the entire term of a loan. Amortization schedules are useful because interest and principal repayment may be treated differently for income tax purposes and it is necessary to keep track of the separate amounts for each. The loan amortization schedule below shows an amortization schedule for a 10-year loan, at an annual rate of 6%, with annual payments.

The formula for the calculation of the PR factors is

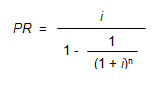
Where:

• PR = Periodic Repayment Factor
• i = Periodic Interest Rate, often expressed as an annual percentage rate
• n = Number of Periods, often expressed in years

In order to calculate the PR factor for 4 years at an annual interest rate of 6%, use the formula below:

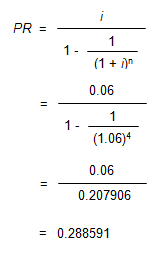
Viewed on a timeline:

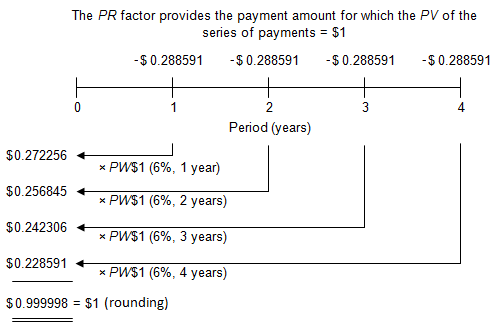
On the timeline, the four payments are negative because from a borrower's perspective they would be cash outflows. The amount borrowed, $1, is positive because from the borrower's perspective it would be a cash inflow.

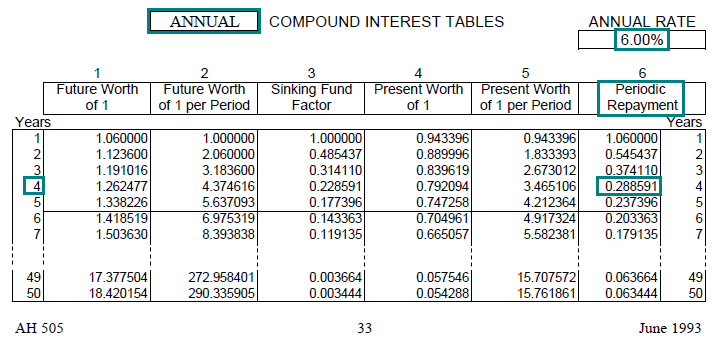
To locate the PR factor go to AH 505, page 33 (opens in a new tab). Go down 4 years and across to column 6. The PR factor is 0.288591.

Example 1:

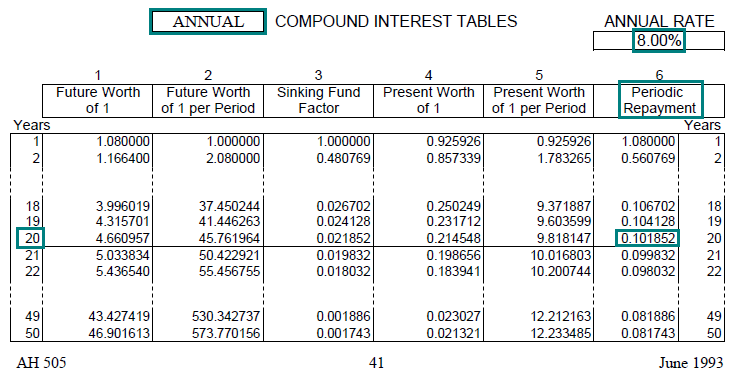
You have just borrowed $50,000, to be repaid in equal annual installments at the end of each of the next 20 years. The annual interest rate is 8%. What is the amount of each annual payment?

Solution:

• PMT = PV × PR (8%, 20 yrs, annual)
• PMT = $50,000 × 0.101852
• PMT = $5,092.60
• Find the annual PR factor (annual compounding) for 8% at a term of 20 years. In AH 505, page 41 (opens in a new tab), go down 20 years and across to column 6 to find the correct factor of 0.101852.
• The annual payment of $5,092.60 is the loan amount of $50,000 multiplied by the PR factor.

Example 2:

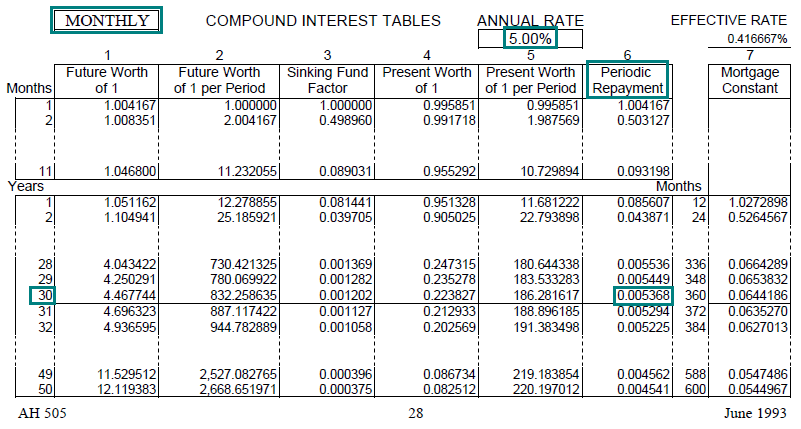
You borrow $200,000 to buy a house, using a fully-amortizing mortgage with monthly payments for 30 years at an annual interest rate of 5%. What is your monthly payment of principal and interest?

Solution:

• PMT = PV × PR (5%, 30 yrs, annual)
• PMT = $200,000 × 0.005368
• PMT = $1,073.60
• Find the monthly PR factor (monthly compounding) for 5% at a term of 30 years. In AH 505, page 28 (opens in a new tab), go down 30 years and across to column 6 to find the correct factor of 0.005368.
• The monthly payment of $1,073.60 is equal to the loan amount multiplied by the monthly PR factor.

Example 3:

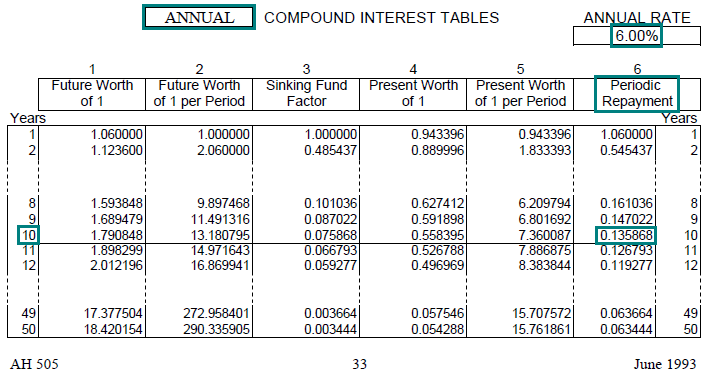
John borrows $75,000 at an annual rate of 6%, repayable in equal annual payments at the end of each of the next 10 years. How much of John's first payment is principal and how much is interest?

Solution:

• PMT = PV × PR (6%, 10 yrs, annual)
• PMT = $75,000 × 0.135868
• PMT = $10,190
• Find the annual PR factor (annual compounding) for 6% at a term of 10 years. In AH 505, page 33 (opens in a new tab), go down 10 years and across to column 6 to find the correct factor of 0.135868.
• The annual payment of $10,190 is the loan amount multiplied by the annual PR factor. The payment is divided between interest and principal repayment.
• The outstanding loan balance for the first year is $75,000, so the interest amount for the first year is $75,000 × 0.06 = $4,500.
• The amount of principal repayment is $10,190 (annual payment) - $4,500 (interest amount) = $5,690.

Example 4:
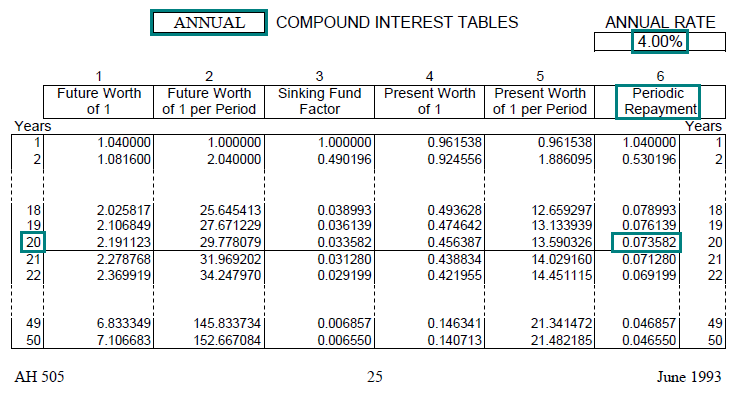
A friend just about ready to retire has $400,000 in his 401k retirement account. If he can earn an annual rate of 4% on the account and wishes to exhaust the fund over 20 years with equal annual withdrawals, how much can he withdraw at the end of each year?

Solution:

• PMT = PV × PR (4%, 20 yrs, annual)
• PMT = $400,000 × 0.073582
• PMT = $29,433
• Find the annual PR factor (annual compounding) for 4% at a term of 20 years. In AH 505, page 25 (opens in a new tab), go down 20 years and across to column 6 to find the correct factor of 0.073582.
• The annual payment of $29,433 is the $400,000 balance in the retirement account multiplied by the annual PR factor.
• The friend could withdraw $29,433 at the end of each year for 20 years, assuming he could earn an annual rate of 4% on the account balance. After 20 years the account would be empty.

The primary use of the PR factor is to provide the amount of the periodic payment necessary to retire a given loan amount. But you can also use it to provide the amount of periodic payment that a given amount will support, assuming an annual interest rate and term, as in this example.

Example 5:

You take out a $100,000 mortgage loan at an annual rate of 6% with monthly payments for 30 years. You plan to sell the property after 12 years. At that time, what will be the outstanding balance (i.e., remaining principal) on the loan?

Solution:

The first step is to calculate the payment amount:

• PMT = PV × PR (6%, 30 yrs, monthly)
• PMT = $100,000 × 0.005996
• PMT = $599.60
• Find the monthly PR factor (monthly compounding) for 6% at a term of 30 years. In AH 505, page 32 (opens in a new tab), go down 30 years and across to column 6 to find the correct monthly factor of 0.005996.
• The monthly payment of $599.60 is the loan amount of $100,000 multiplied by the monthly PR factor.

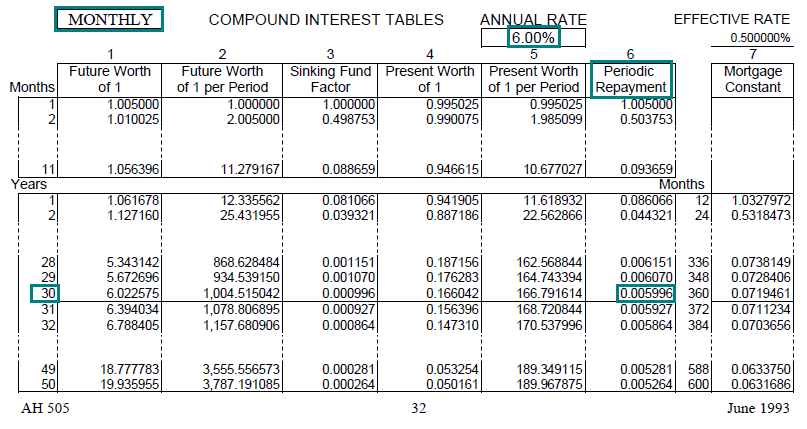
The remaining balance of an amortizing loan is the present value of the loan's remaining payments discounted at the loan's contract rate of interest. The second step is to discount the remaining 18 years of monthly payments using the PW$1/P factor at 6%.

• PV = PMT × PW$1/P (6%, 18 yrs, monthly)
• PV = $599.60 × 131.897876
• PV = $79,085.97
• Find the monthly PW$1/P factor (monthly compounding) for 6% for 18 years. In AH 505, page 32 (opens in a new tab), go down 18 years and across to column 5 to find the correct monthly PW$1/P factor of 131.897876.
• The remaining loan balance of $79,085.97 is the payment amount of $599.60 multiplied by the PW$1/P factor.