Time Value of Money – Six Functions of a Dollar
Lesson 9 – Frequency of Compounding

Appraisal Training: Self-Paced Online Learning Session

This lesson discusses the frequency of compounding and its affect on the present and future values using the compound interest functions presented in Assessors’ Handbook Section 505 (AH 505), Capitalization Formulas and Tables. The lesson:

  • Explains compounding frequency and intra-year compounding
  • Demonstrated calculation of FW$1 and PW$1 factors given monthly compounding
  • Concludes with generalizations with respect to frequency of compounding and future and present value
Open All Close All

Up to this point, we generally have assumed that interest was calculated at the end of each year, based on the principal balance at the beginning of the year and the annual interest rate. That is, we have assumed that interest was compounded (or discounted) on an annual basis, and in solving problems we have used the annual compounding pages in AH 505 (opens in a new tab).

Compounding interest more than once a year is called “intra-year compounding”. Interest may be compounded on a semi-annual, quarterly, monthly, daily, or even continuous basis. When interest is compounded more than once a year, this affects both future and present-value calculations.

With intra-year compounding, the periodic interest rate, instead of being the stated annual rate, becomes the stated annual rate divided by the number of compounding periods per year. The number of periods, instead of being the number of years, becomes the number of compounding periods per year multiplied by the number of years.

As shown in the following table:

How to Calculate the Number of Compounding Periods and the Periodic Interest Rate
Compounding Frequency Number of Periods, n Periodic Rate, i
Annual years i = annual interest rate
Quarterly quarters (years × 4) i = annual interest rate ÷ 4
Monthly months (years × 12) i = annual interest rate ÷ 12
Daily days (years × 365) i = annual interest rate ÷ 365

With monthly compounding, for example, the stated annual interest rate is divided by 12 to find the periodic (monthly) rate, and the number of years is multiplied by 12 to determine the number of (monthly) periods.

In lesson 2, we calculated the annual FW$1 factor at a stated annual rate of 6% for 4 years with annual compounding. The resulting factor was 1.262477.

Now let's calculate the FW$1 for an annual rate of 6% for 4 years, but with monthly compounding. In this case, the periodic monthly rate is 0.5% (one-half of one percent per month, 6% ÷ 12), and the number of monthly compounding periods is 48 (12 periods/year × 4 years).

In order to calculate the FW$1 factor for 4 years at an annual interest rate of 6%, with monthly compounding, use the formula below:

  • FW$1 = (1 + i)n
  • FW$1 = (1 + 0.5%)48
  • FW$1 = (1 + 0.005)48
  • FW$1 = (1.005)48
  • FW$1 = 1.270489

The FW$1 factor with monthly compounding, 1.270489, is slightly greater than the factor with annual compounding, 1.262477. If we had invested $100 at an annual rate of 6% with monthly compounding we would have ended up with $127.05 four years later; with annual compounding we would have ended up with $126.25.

AH 505 contains separate sets of compound interest factors for annual and monthly compounding. Factors for annual compounding are on the odd-numbered pages; factors for monthly compounding are on the even-numbered pages.The FW$1 factor for 4 years at an annual interest rate of 6%, with monthly compounding, is in AH 505, page 32 (opens in a new tab) (monthly page).

Cells of note are highlighted. MONTHLY COMPOUND INTEREST TABLES – Months

Note this value.ANNUAL RATE 6.00%

Note this value.EFFECTIVE RATE
0.500000%
Months Future Worth of 1 Future Worth of 1 per Period Sinking Fund Factor Present Worth of 1 Present Worth of 1 per Period Periodic Repayment
1 1.005000 1.000000 1.000000 0.995025 0.995025 1.005000
2 1.010025 2.005000 0.498753 0.990075 1.985099 0.503753
3 1.015075 3.015025 0.331672 0.985149 2.970248 0.336672
4 1.020151 4.030100 0.248133 0.980248 3.950496 0.253133
5 1.025251 5.050251 0.198010 0.975371 4.925866 0.203010
6 1.030378 6.075502 0.164595 0.970518 5.896384 0.169595
7 1.035529 7.105879 0.140729 0.965690 6.862074 0.145729
8 1.040707 8.141409 0.122829 0.960885 7.822959 0.127829
9 1.045911 9.182116 0.108907 0.956105 8.779064 0.113907
10 1.051140 10.228026 0.097771 0.951348 9.730412 0.102771
11 1.056396 11.279167 0.088659 0.946615 10.677027 0.093659

Cells of note are highlighted. MONTHLY COMPOUND INTEREST TABLES – Years

Note this value.ANNUAL RATE 6.00%
Years Note this text.Future Worth of 1 Future Worth of 1 per Period Sinking Fund Factor Present Worth of 1 Present Worth of 1 per Period Periodic Repayment Months Mortgage Constant
1 1.061678 12.335562 0.081066 0.941905 11.618932 0.086066 12 1.0327972
2 1.127160 25.431955 0.039321 0.887186 22.562866 0.044321 24 0.5318473
3 1.196681 39.336105 0.025422 0.835645 32.871016 0.030422 36 0.3650632
Note this value.4 Note this value.1.270489 54.097832 0.018485 0.787098 42.580318 0.023485 48 0,2818203
5 1.348850 69.770031 0.014333 0.741372 51.725561 0.019333 60 0.2319936
6 1.432044 86.408856 0.011573 0.698302 60.339514 0.016573 72 0.1988747

In lesson 3, we calculated the PW$1 factor at an annual rate of 6% for 4 years with annual compounding. The resulting factor was 0.792094.

Let's calculate the PW$1 factor for 4 years at an annual interest rate of 6%, with monthly compounding. In this case, the periodic monthly rate is 0.5% (one-half of one percent per month, 6% ÷ 12), and the number of monthly compounding periods is 48 (12 periods/year × 4 years).

In order to calculate the PW$1 factor for 4 years at an annual interest rate of 6%, with monthly compounding, use the formula below:

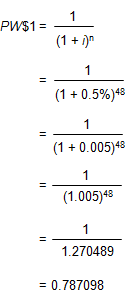
an equation showing that the present worth of one dollar factor is equal to 1 over the quantity 1 plus i raised to the power n. The value for i is 0.005 (0.5 percent, the annual periodic rate), the value for n is 48 and the final result is 0.787098.

The PW$1 factor for 4 years at an annual interest rate of 6%, with monthly compounding, can be found in AH 505, page 32 (opens in a new tab). The amount of the factor is 0.787098.

Cells of note are highlighted. MONTHLY COMPOUND INTEREST TABLES – Months

Note this value.ANNUAL RATE 6.00%

Note this value.EFFECTIVE RATE
0.500000%
Months Future Worth of 1 Future Worth of 1 per Period Sinking Fund Factor Present Worth of 1 Present Worth of 1 per Period Periodic Repayment
1 1.005000 1.000000 1.000000 0.995025 0.995025 1.005000
2 1.010025 2.005000 0.498753 0.990075 1.985099 0.503753
3 1.015075 3.015025 0.331672 0.985149 2.970248 0.336672
4 1.020151 4.030100 0.248133 0.980248 3.950496 0.253133
5 1.025251 5.050251 0.198010 0.975371 4.925866 0.203010
6 1.030378 6.075502 0.164595 0.970518 5.896384 0.169595
7 1.035529 7.105879 0.140729 0.965690 6.862074 0.145729
8 1.040707 8.141409 0.122829 0.960885 7.822959 0.127829
9 1.045911 9.182116 0.108907 0.956105 8.779064 0.113907
10 1.051140 10.228026 0.097771 0.951348 9.730412 0.102771
11 1.056396 11.279167 0.088659 0.946615 10.677027 0.093659

Cells of note are highlighted. MONTHLY COMPOUND INTEREST TABLES – Years

Note this value.ANNUAL RATE 6.00%
Years Future Worth of 1 Future Worth of 1 per Period Sinking Fund Factor Note this text.Present Worth of 1 Present Worth of 1 per Period Periodic Repayment Months Mortgage Constant
1 1.061678 12.335562 0.081066 0.941905 11.618932 0.086066 12 1.0327972
2 1.127160 25.431955 0.039321 0.887186 22.562866 0.044321 24 0.5318473
3 1.196681 39.336105 0.025422 0.835645 32.871016 0.030422 36 0.3650632
Note this value.4 1.270489 54.097832 0.018485 Note this value.0.787098 42.580318 0.023485 48 0,2818203
5 1.348850 69.770031 0.014333 0.741372 51.725561 0.019333 60 0.2319936
6 1.432044 86.408856 0.011573 0.698302 60.339514 0.016573 72 0.1988747

The following two generalizations can be made with respect to frequency of compounding and future and present values:

  • When interest is compounded more than once a year, a future value will always be higher than it would have been with annual compounding, all else being equal.
  • When interest is compounded more than once a year, a present value will always be lower than it would have been with annual compounding, all else being equal.

Thus, with our examples for the FW$1 and the PW$1:

  • Given FW$1, at a rate of 6%, for a term of 4 years: 1.270489 (compounded monthly) > 1.262477 (compounded annually)
  • Given PW$1, at a rate of 6%, for a term of 4 years: 0.787098 (compounded monthly < 0.792094 (compounded annually)

We would have obtained similar results with FW$1/P and PW$1/P, respectively.

Most appraisal problems involve annual payments and require the use of annual factors. Monthly factors are also useful because most mortgage loans are based on monthly payments, and it is often necessary to make mortgage calculations as part of an appraisal problem.

For other compounding periods, the factors for which are not included in AH 505, the appraiser can calculate the desired factor from the appropriate compound interest formula. As noted, AH 505 contains factors for annual and monthly compounding only.

Next Lesson