Time Value of Money – Six Functions of a Dollar
Lesson 2 – Future Worth of $1
Appraisal Training: Self-Paced Online Learning Session
This lesson discusses the Future Worth of $1 (FW$1); one of six compound interest functions presented in Assessors' Handbook Section 505 (AH 505), Capitalization Formulas and Tables. This lesson:
- Explains the FW$1 function's meaning and purpose
- Provides the formula for FW$1 factors
- Contains practical examples of how to apply the FW$1 factor
- Explains the Rule of 72
- Shows how to calculate the future value of multiple payments
FW$1: Meaning and Purpose
The FW$1 is the amount to which $1 will grow at periodic interest rate i after n periods, assuming the payment of $1 occurs at the beginning of the first period.
The FW$1 is used to compound a single present amount to its future amount. The FW$1 factors are in column 1 of AH 505 (opens in a new tab).
The future worth of 1 factor (FW$1) is based on the premise that $1 deposited at the beginning of a period earns interest during the period and becomes part of the principal at the beginning of the next period. This continues for the number of periods in the problem.
Formula for Calculating FW$1 Factors
The formula for the calculation of the FW$1 factors is
FW$1 = (1 + i)n
Where:
- FW$1 = Future Worth of $1 Factor
- i = Periodic Interest Rate, often expressed as an annual percentage rate
- n = Number of Periods, often expressed in years
All of the other compound interest formulas published in AH 505 are derived from the basic compounding expression in the FW$1 factor, (1 + i)n. As we will see, this mathematical expression is the basic building block of all the other compound interest formulas.
The periodic interest rate, i, must match the compounding period, n (this holds for all compound interest functions). For example, if n is stated in years, indicating annual compounding, i must be stated as an annual rate; if n is stated in months, indicating monthly compounding, i must be stated as a monthly rate.
For now, we will assume annual compounding, so our periods, n, will be in years and the periodic interest rate, i, will be the annual percentage rate. Later, we will introduce the concept of more than one compounding period per year (monthly, quarterly, etc.).
In order to calculate the annual FW$1 factor for 4 years at an annual interest rate of 6%, use the formula below:
- FW$1 = (1 + i)n
- FW$1 = (1 + 0.06)4
- FW$1 = (1.06)4
- FW$1 = 1.262477
Viewed on a timeline:
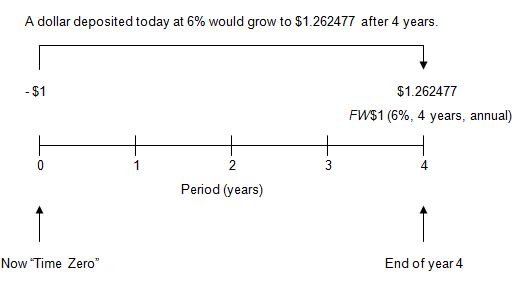
On the timeline, the initial deposit of $1 is shown as negative because from the point of view of a depositer it would be a cash outflow. The future value is shown as positive because it would be a cash inflow. The depositor gives up money now in order to receive money later.
To locate the FW$1 factor go to AH 505, page 33 (opens in a new tab). Go down 4 years and across to column 1. The FW$1 factor is 1.262477.
In most problems, we don't want the FW$1; we want the future worth of some other amount that has been deposited or invested. To put it another way, we want to use the FW$1 factor to solve a TVM problem. When working problems, we will use the notation shown below. Don't worry too much about the notation now. Using it will become easier as we work problems throughout the lessons.
Practical Applications of FW$1
Example 1:
You deposit $2,000 today at an annual interest rate of 6%. How much will you have at the end of 10 years, assuming annual compounding?
Solution:
- FV = PV × FW$1 (6%, 10 yrs, annual)
- FV = $2,000 × 1.790848
- FV = $3,582
- Find the annual FW$1 factor (annual compounding) for 6% at a term of 10 years. In AH 505, page 33 (opens in a new tab), go down 10 years and across to column 1 to find the correct factor of 1.790848.
- The future value of $3,582 is equal to the present value of $2,000 multiplied by the factor.
Example 2:
The Jones family places $100,000 in an investment that will provide an annual rate of return of 5%. What will the investment be worth in 2 years?
Solution:
- FV = PV × FW$1 (5%, 2 yrs, annual)
- FV = $100,000 × 1.102500
- FV = $110,250
- Find the annual FW$1 factor (annual compounding) for 5% at a term of 2 years. In AH 505, page 29 (opens in a new tab), go down 2 years and across to column 1 to find the correct factor of 1.102500.
- The future value of $110,250 is equal to the present value of $100,000 multiplied by the factor.
Example 3:
You have $450,000 to invest and can earn an annual interest rate of 7.50%. How much will your investment be worth in 10 years?
Solution:
- FV = PV × FW$1 (7.50%, 10 yrs, annual)
- FV = $450,000 × 2.061032
- FV = $927,464
- Find the annual FW$1 factor (annual compounding) for 7.50% at a term of 10 years. In AH 505, page 39 (opens in a new tab), go down 10 years and across to column 1 to find the correct factor of 2.061032.
- The future value of $927,464 is equal to the present value of $450,000 multiplied by the factor.
Example 4:
A given product costs $500 today. The cost of the product is expected to rise at an annual rate of 10%. How much will the product cost in 5 years?
Solution:
- FV = PV × FW$1 (10%, 5 yrs, annual)
- FV = $500 × 1.610510
- FV = $805
- Find the annual FW$1 factor (annual compounding) for 10% at a term of 5 years. In AH 505, page 49 (opens in a new tab), go down 5 years and across to column 1 to find the correct factor of 1.610510.
- The future value of $805 is equal to the present value of $500 multiplied by the factor.
Example 5:
Approximately how long does it take a given amount to grow to 10 times its original amount, given an annual interest rate of 5% with annual compounding?
Solution:
- Use the compound interest tables to estimate the answer by inspecting the tables.
- On the annual page for 5% (AH 505, page 29 [opens in a new tab]), inspect the FW$1 column (column 1) to find a factor that is approximately equal to 10 (FV ÷ PV = 10 ÷ 1).
- The answer is slightly greater than 47 years (the factor for 47 years is 9.905971).
“Rule of 72”
The Rule of 72 is a rule of thumb that is closely related to the FW$1 factor. The rule assumes annual compounding.
The Rule of 72 can be used to estimate either of the following:
- The number of years it would take for an amount to double at a given annual interest rate, or
- The annual interest rate, if an amount has doubled in a given number of years.
The formula for the Rule of 72 is:
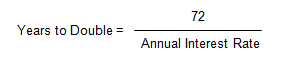
Or, transposing:
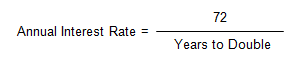
Note: When using the Rule of 72, the annual interest rates are stated as percentages, not as decimals.
The smaller the difference between the factors of 72 (i.e., the number of years and the annual interest rate) the more accurate the estimate. For example, when the factors are 9 and 8, the estimate is more accurate than when the factors are 36 and 2.
Practical Applications of “Rule of 72”
Example 1:
You deposit $1,000 in an account that pays an annual interest rate of 6%. Approximately how long will it take this deposit to grow to $2,000?
Solution:
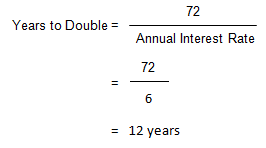
The estimate may be confirmed using the compound interest tables in AH 505, page 33 (opens in a new tab), column 1. At 12 years, the FW$1 factor is approximately equal to 2, indicating a doubling (the actual factor is 2.012196).
Example 2:
Eight years ago you received a small inheritance that you deposited in a savings account. The amount has now doubled. What compound annual interest rate have you earned over the past 8 years?
Solution:
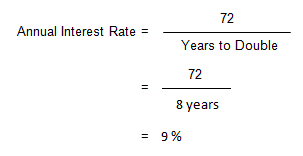
To confirm the estimate, search in AH 505 for the annual rate at which the FW$1 factor for 8 years is approximately equal to 2, indicating a doubling. In AH 505, page 45 (opens in a new tab), column 1, the FW$1 factor at 8 years is approximately equal to 2 (the actual factor is 1.992563).
Example 3:
You've purchased a house that you think will double in value in 10 years. At what annual compound rate will the property have appreciated?
Solution:
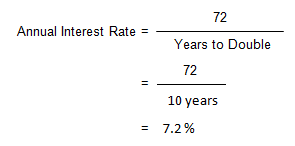
At an annual rate of 7.00% the FW$1 factor for 10 years is 1.967151 (AH 505, page 37 [opens in a new tab]).
At an annual rate of 7.50% the FW$1 factor for 10 years is 2.061032 (AH 505, page 39 [opens in a new tab]).
Interpolating, the annual rate at which the FW$1 factor is 2, is somewhere between 7.00 and 7.50%, approximately 7.2%.
Multiple Payments and FW$1
We have calculated the future value of single amounts or payments, using the FW$1 factor.
Many problems involve more than one payment, making it necessary to calculate the future value of multiple payments–that is, the future value of a stream of payments. Determining the future value of multiple payments is a straightforward extension of the single-payment situation.
When we calculated the future value of a single amount or payment, we multiplied the payment by the appropriate FW$1 factor. This compounded the payment to its future value.
If there is more than one payment, we must multiply each payment by the appropriate FW$1 factor and add up all of the future values. The sum of the future values is the total future value of the stream of payments.
Practical Applications of FW$1 with Multiple Payments
Example 1
You plan to make the following three deposits into a savings account:
- $10,000 at the end of the first year
- $15,000 at the end of the second year
- $20,000 at the end of the third year
At an annual interest rate of 5%, how much will you have in the account at the end of the third year (i.e., what is the total future value of all three payments)?
Solution:
Calculate the future value of each payment as of the end of year 3 using the appropriate FW$1 factor (AH 505, page 29 [opens in a new tab], column 1) and add those future values. This sum is the future value of all three payments at the end of 3 years.
Thus:
| Payment | FW$1 Factor | Future Value |
|---|---|---|
| $10,000 × | 1.102500 (FW$1, 5%, 2 years) = | $11,025 |
| $15,000 × | 1.050000 (FW$1, 5%, 1 year) = | $15,750 |
| $20,000 × | 1.0 (no compounding) = | $20,000 |
| Total future value at end of year 3 = | $46,775 | |
The first payment is compounded forward for two periods (years); the second payment for one period (year); and the final payment, which itself at the end of year 3, requires no compounding.
Viewed on a Timeline:
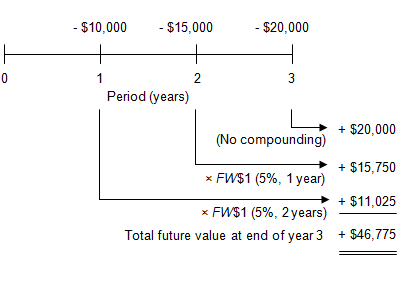
On the timeline, the deposits are shown as negative because from the perspective of the depositor they represent cash outflows, and the resulting future values are shown as positive because they represent cash inflows at the end of year 3.

