Time Value of Money – Six Functions of a Dollar
Lesson 8 – Mortgage Constant
Appraisal Training: Self-Paced Online Learning Session
This lesson discusses the Mortgage Constant (MC), which is listed in the monthly tables of Assessors' Handbook Section 505 (AH 505), Capitalization Formulas and Tables. The lesson:
- Explains the meaning and purpose of the MC
- Explains how to find MC factors in AH 505 and calculate MC factors
- Contains practical examples of how to apply the MC factor
MC: Meaning and Purpose
The MC factor provides the annualized payment amount per $1 of loan amount for a fully-amortized loan with monthly compounding and payments.
Mathematically, the MC factor is simply the monthly PR factor multiplied by 12. The MC factor is also known as the annualized mortgage constant or constant annual percent. The MC factors are in column 7 of the monthly pages of AH 505 (opens in a new tab).
Calculating MC Factors
To locate the MC factor for a term of 30 years at an annual interest rate of 6%, go to AH 505, page 32 (opens in a new tab), go down 30 years and across to column 7. The MC factor is 0.0719461. MC factors are found in Column 7 of the monthly tables only.
| Months | Future Worth of 1 | Future Worth of 1 per Period | Sinking Fund Factor | Present Worth of 1 | Present Worth of 1 per Period | Periodic Repayment |
|---|---|---|---|---|---|---|
| 1 | 1.005000 | 1.000000 | 1.000000 | 0.995025 | 0.995025 | 1.005000 |
| 2 | 1.010025 | 2.005000 | 0.498753 | 0.990075 | 1.985099 | 0.503753 |
| 3 | 1.015075 | 3.015025 | 0.331672 | 0.985149 | 2.970248 | 0.336672 |
| 4 | 1.020151 | 4.030100 | 0.248133 | 0.980248 | 3.950496 | 0.253133 |
| 5 | 1.025251 | 5.050251 | 0.198010 | 0.975371 | 4.925866 | 0.203010 |
| 6 | 1.030378 | 6.075502 | 0.164595 | 0.970518 | 5.896384 | 0.169595 |
| 7 | 1.035529 | 7.105879 | 0.140729 | 0.965690 | 6.862074 | 0.145729 |
| 8 | 1.040707 | 8.141409 | 0.122829 | 0.960885 | 7.822959 | 0.127829 |
| 9 | 1.045911 | 9.182116 | 0.108907 | 0.956105 | 8.779064 | 0.113907 |
| 10 | 1.051140 | 10.228026 | 0.097771 | 0.951348 | 9.730412 | 0.102771 |
| 11 | 1.056396 | 11.279167 | 0.088659 | 0.946615 | 10.677027 | 0.093659 |
You can confirm that the MC factor is the monthly periodic repayment factor multiplied by 12: 0.005996 × 12 = 0.071952 (small difference due to rounding).
This means that for every $1 of loan amount, the annual total of the 12 monthly payments will be $0.071952 (or $0.072). Or, stating it another way, the sum of the 12 monthly payments will be equal to 7.1952% (or 7.2%) of the loan amount.
We could have calculated the MC factor by first calculating the monthly PR factor and then multiplying it by 12 (note that both i and n must be expressed in months, not years) using the formula below:
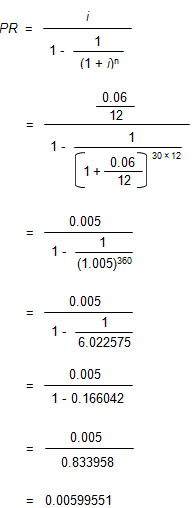
- MC = PR × 12
- MC = 0.00599551 × 12
- MC = 0.0719461
Practical Applications of MC
Example 1:
A buyer takes out a mortgage loan for $250,000 at an annual rate of 8% with monthly payments for 30 years. What percentage of the original loan amount will she pay on an annualized basis?
Solution:
- The problem simply asks for the MC factor, which we can look up directly in AH 505.
- Go to AH 505, page 40 (opens in a new tab), column 7, 30 years, to find the MC factor of 0.0880517. This is equivalent to 8.80517%
| Months | Future Worth of 1 | Future Worth of 1 per Period | Sinking Fund Factor | Present Worth of 1 | Present Worth of 1 per Period | Periodic Repayment |
|---|---|---|---|---|---|---|
| 1 | 1.006667 | 1.000000 | 1.000000 | 0.993377 | 0.993377 | 1.006667 |
| 2 | 1.013378 | 2.006667 | 0.498339 | 0.986799 | 1.980176 | 0.505006 |
| 3 | 1.020134 | 3.020044 | 0.331121 | 0.980264 | 2.960440 | 0.337788 |
| 4 | 1.026935 | 4.040178 | 0.247514 | 0.973772 | 3.934212 | 0.254181 |
| 5 | 1.033781 | 5.067113 | 0.197351 | 0.967323 | 4.901535 | 0.204018 |
| 6 | 1.040673 | 6.100893 | 0.163910 | 0.960917 | 5.862452 | 0.170577 |
| 7 | 1.047610 | 7.141566 | 0.140025 | 0.954553 | 6.817005 | 0.146692 |
| 8 | 1.054595 | 8.189176 | 0.122112 | 0.948232 | 7.765237 | 0.128779 |
| 9 | 1.061625 | 9.243771 | 0.108181 | 0.941952 | 8.707189 | 0.114848 |
| 10 | 1.068703 | 10.305396 | 0.097037 | 0.935714 | 9.642903 | 0.103703 |
| 11 | 1.075827 | 11.374099 | 0.087919 | 0.929517 | 10.572420 | 0.094586 |
One can confirm the answer by calculating the monthly payment, multiplying it by 12, and dividing this product by the original loan amount (difference between factor and table and calculation due to rounding):
- PMT = PV × PR (8%, 30 years, annual)
- PMT = $250,000 × 0.007338
- PMT = $1,834.50
- MC = (PMT × 12) ÷ PV
- MC = ($1,834.50 × 12) ÷ $250,000
- MC = $22,014 ÷ $250,000
- MC = 0.088056, or 8.8056%
Example 2:
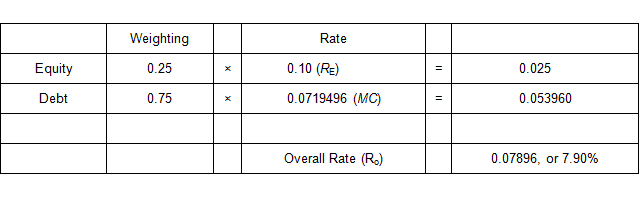
In the band of investment method for deriving an overall capitalization rate (RO),
the rate is a weighted average of the equity dividend rate (RE) and the mortgage constant (MC), with the weightings based on the respective proportions of equity and debt.
The current equity dividend rate is 10% and a loan can be obtained at an annual interest
rate of 6% with monthly payments for 30 years at a loan-to-value ratio of 75%.
Calculate an overall capitalization rate using the band of investment.
Solution:
- Find the MC factor in AH 505, page 32 (opens in a new tab), column 7, for 30 years. The correct MC factor is 0.0719461.
- Use the band of investment method to estimate the overall rate (RO) using the calculation shown in the table below.
- The estimated overall capitalization rate (RO) is 7.90%.
| Months | Future Worth of 1 | Future Worth of 1 per Period | Sinking Fund Factor | Present Worth of 1 | Present Worth of 1 per Period | Periodic Repayment |
|---|---|---|---|---|---|---|
| 1 | 1.005000 | 1.000000 | 1.000000 | 0.995025 | 0.995025 | 1.005000 |
| 2 | 1.010025 | 2.005000 | 0.498753 | 0.990075 | 1.985099 | 0.503753 |
| 3 | 1.015075 | 3.015025 | 0.331672 | 0.985149 | 2.970248 | 0.336672 |
| 4 | 1.020151 | 4.030100 | 0.248133 | 0.980248 | 3.950496 | 0.253133 |
| 5 | 1.025251 | 5.050251 | 0.198010 | 0.975371 | 4.925866 | 0.203010 |
| 6 | 1.030378 | 6.075502 | 0.164595 | 0.970518 | 5.896384 | 0.169595 |
| 7 | 1.035529 | 7.105879 | 0.140729 | 0.965690 | 6.862074 | 0.145729 |
| 8 | 1.040707 | 8.141409 | 0.122829 | 0.960885 | 7.822959 | 0.127829 |
| 9 | 1.045911 | 9.182116 | 0.108907 | 0.956105 | 8.779064 | 0.113907 |
| 10 | 1.051140 | 10.228026 | 0.097771 | 0.951348 | 9.730412 | 0.102771 |
| 11 | 1.056396 | 11.279167 | 0.088659 | 0.946615 | 10.677027 | 0.093659 |

