Time Value of Money – Six Functions of a Dollar
Lesson 4 – Future Worth of $1 Per Period
Appraisal Training: Self-Paced Online Learning Session
This lesson discusses the Future Worth of $1 per Period (FW$1/P); one of six compound interest functions presented in Assessors' Handbook Section 505 (AH 505), Capitalization Formulas and Tables. The lesson:
- Explains the function's meaning and purpose
- Provides the formula for the calculation of FW$1/P factor
- Contains practical examples of how to apply the FW$1/P factor
FW$1/P: Meaning and Purpose
The FW$1/P factor is the amount to which a series of periodic payments of $1 will compound at periodic interest rate i over n periods, assuming payments occur at the end of each period.
The FW$1/P factor is used to compound a series of periodic equal payments to their future value. The FW$1/P factors are in column 2 of AH 505 (opens in a new tab).
FW$1/P factors are applicable to ordinary annuity problems. An annuity may be defined as a series of periodic payments, usually equal in amount, and payable at the end of the period. (See Lesson 10 for further discussion of annuities.)
Formula for Calculating FW$1/P
The formula for the calculation of the FW$1/P factors is
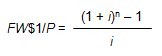
Where:
- FW$1/P = Future Worth of $1 per Period Factor
- i = Periodic Interest Rate, often expressed as an annual percentage rate
- n = Number of Periods, often expressed in years
In order to calculate the annual FW$1/P factor for 4 years at an annual interest rate of 6%, use the formula below:
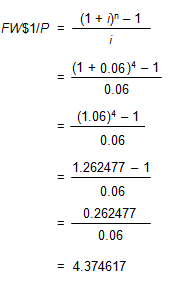
Viewed on a timeline:
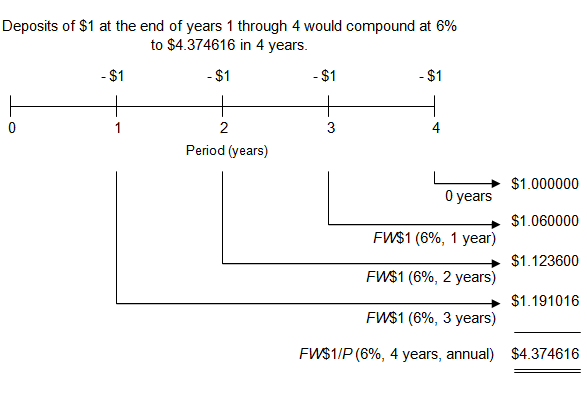
On the timeline, the deposits of $1 are shown as negative because from the point of view of a depositor they would be cash outflows. The future values are shown as positive because they would be cash inflows. The depositor gives up money at the end of each year in order to receive money at the end of year 4.
To locate the FW$1/P factor, go to AH 505, page 33 (opens in a new tab), go down 4 years and across to column 2. The correct factor is 4.374616.
Practical Applications of FW$1/P
Example 1:
What is the future value of 3 payments of $1,000 with the payments made at the end of each of the next 3 years? (Assume an annual interest rate of 10%.)
Solution:
- FV = PMT × FW$1/P (10%, 3 yrs, annual)
- FV = $1,000 × 3.310000
- FV = $3,310
- Find the annual FW$1/P factor (annual compounding) for 10% and a term of 3 years. In AH 505, page 49 (opens in a new tab), go down 3 years and across to column 2 to find the correct factor of 3.310000.
- The future value of $3,310 is equal to the periodic payment of $1,000 multiplied by the factor.
Viewed on a timeline:
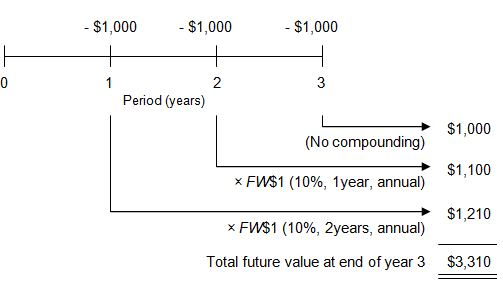
The problem could have been solved by using the FW$1 factor applicable to each payment, but it would have taken 4 calculations.
- End-of-year 1 payment FW = $1,000 × 1.210000 = $1,210
- End-of-year 2 payment FW = $1,000 × 1.100000 = $1,100
- End-of-year 3 payment FW = $1,000 × 1.000000 (no compounding) = $1,000
- Total value at end of year 3 = $3,310
Notes
- 1.210000 = FW$1 (10%, 2 years, annual) (AH 505, page 49, column 1)
- 1.100000 = FW$1 (10%, 1 year, annual) (AH 505, page 49, column 1)
Using the FW$1/P annuity factor simplifies the calculation. Annuity factors are essentially shortcuts that can be used when cash flows or payments are equal and at regular intervals.
Example 2:
You deposit $13,000 at the end of each year for 23 years. If the account earns an annual rate of 7.50%, compounded annually, how much will be in the account after 23 years?
Solution:
- FV = PMT × FW$1/P (7.50%, 23 yrs, annual)
- FV = $13,000 × 57.027895
- FV = $741,363
- Find the annual FW$1/P factor (annual compounding) for 7.50% and a term of 23 years. In AH 505, page 39 (opens in a new tab), go down 23 years and across to column 2 to find the correct factor of 57.027895.
- The future value of $741,363 is equal to the payment of $13,000 multiplied by the factor.
Example 3:
Mr. Foresight deposits $1,500 at the end of each month into a retirement account that returns an annual rate of 6%, compounded monthly. How much will he have after 10 years? After 30 years?
Solution:
After 10 years:
- FV = PMT × FW$1/P (6%, 10 yrs, monthly)
- FV = $1,500 × 163.879347
- FV = $245,819
After 30 years:
- FV = PMT × FW$1/P (6%, 30 yrs, monthly)
- FV = $1,500 × 1,004.515042
- FV = $1,506,773
- Find the monthly FW$1/P factors (monthly compounding) for 6% at terms of 10 and 30 years, respectively. In AH 505, page 32 (opens in a new tab), go to column 2, to find the correct factors of 163.879347 and 1,004.515042.
- The future values of $245,819 and $1,506,773, respectively, are equal to the payment of $1,500 multiplied by the appropriate factors. What a difference 20 years makes.
| Months | Future Worth of 1 | Future Worth of 1 per Period | Sinking Fund Factor | Present Worth of 1 | Present Worth of 1 per Period | Periodic Repayment |
|---|---|---|---|---|---|---|
| 1 | 1.005000 | 1.000000 | 1.000000 | 0.995025 | 0.995025 | 1.005000 |
| 2 | 1.010025 | 2.005000 | 0.498753 | 0.990075 | 1.985099 | 0.503753 |
| 3 | 1.015075 | 3.015025 | 0.331672 | 0.985149 | 2.970248 | 0.336672 |
| 4 | 1.020151 | 4.030100 | 0.248133 | 0.980248 | 3.950496 | 0.253133 |
| 5 | 1.025251 | 5.050251 | 0.198010 | 0.975371 | 4.925866 | 0.203010 |
| 6 | 1.030378 | 6.075502 | 0.164595 | 0.970518 | 5.896384 | 0.169595 |
| 7 | 1.035529 | 7.105879 | 0.140729 | 0.965690 | 6.862074 | 0.145729 |
| 8 | 1.040707 | 8.141409 | 0.122829 | 0.960885 | 7.822959 | 0.127829 |
| 9 | 1.045911 | 9.182116 | 0.108907 | 0.956105 | 8.779064 | 0.113907 |
| 10 | 1.051140 | 10.228026 | 0.097771 | 0.951348 | 9.730412 | 0.102771 |
| 11 | 1.056396 | 11.279167 | 0.088659 | 0.946615 | 10.677027 | 0.093659 |
Example 4:
Mrs. Foresight invests $20,000 in a 401k account at the end of each year for 10 years, earning an annual rate of 7%, compounded annually. At the end of 10 years, she invests the lump-sum balance for another 10 years, earning an annual rate of 8%, compounded annually. How much will Mrs. Foresight have at the end of 20 years?
(Hint: This problem combines the FW$1/P and the FW$1)
Solution:
This is a two-part problem.
Part I: First 10 years
- FV = PMT × FW$1/P (7%, 10 yrs, annual)
- FV = $20,000 × 13.816448
- FV = $276,329
- Find the correct FW$1/P factor (AH 505, page 37 [opens in a new tab], column 2) to calculate the future value of the payments after the first 10 years; the correct factor is 13.816448.
- After the first 10 years the future value is $276,329.
Part II: End of 20 years (final answer)
- FV = PMT × FW$1 (8%, 10 yrs, annual)
- FV = $276,329 × 2.158925
- FV = $596,574
- Use the future value calculated in Part I ($276,329) as the present value in the next calculation.
- Find the FW$1 factor (AH 505, page 41 [opens in a new tab], column 1); the correct factor is 2.158925.
- Calculate the final future value (at the end of 20 years) using the formula:
Example 5:
You want to save $8,000 to buy a car. You will deposit $185.71 at the end of every month. Your first deposit will be a month from today. If your account pays an annual interest rate of 12%, compounded monthly, approximately how many months will it take to save $8,000?
Solution:
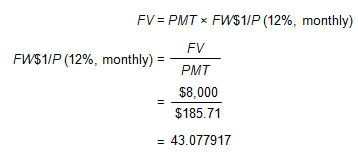
- In AH 505, page 56 (opens in a new tab), column 2, find the FW$1/P factor that is closest to 43.077917; the correct factor is 43.076878.
- In order to save $8,000, you will need to deposit $185.71 for approximately 3 years or 36 months.
| Months | Future Worth of 1 | Future Worth of 1 per Period | Sinking Fund Factor | Present Worth of 1 | Present Worth of 1 per Period | Periodic Repayment |
|---|---|---|---|---|---|---|
| 1 | 1.010000 | 1.000000 | 1.000000 | 0.990099 | 0.990099 | 1.010000 |
| 2 | 1.020100 | 2.010000 | 0.497512 | 0.980296 | 1.970395 | 0.507512 |
| 3 | 1.030301 | 3.030100 | 0.330022 | 0.970590 | 2.940985 | 0.340022 |
| 4 | 1.040604 | 4.060401 | 0.246281 | 0.960980 | 3.901966 | 0.256281 |
| 5 | 1.051010 | 5.101005 | 0.196040 | 0.951466 | 4.853431 | 0.206040 |
| 6 | 1.061520 | 6.152015 | 0.162548 | 0.942045 | 5.795476 | 0.172548 |
| 7 | 1.072135 | 7.213535 | 0.138628 | 0.932718 | 6.728195 | 0.148628 |
| 8 | 1.082857 | 8.285671 | 0.120690 | 0.923483 | 7.651678 | 0.130690 |
| 9 | 1.093685 | 9.368527 | 0.106740 | 0.914340 | 8.566018 | 0.116740 |
| 10 | 1.104622 | 10.462213 | 0.095582 | 0.905287 | 9.471305 | 0.105582 |
| 11 | 1.115668 | 11.566835 | 0.086454 | 0.896324 | 10.367628 | 0.096454 |

